Calculate the Formula of a Parabola from its Function

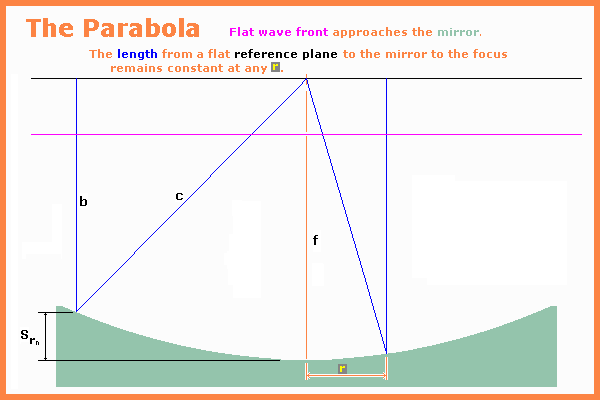
The waves actually come from a distant star but for our calculations we assume the waves pass the focal plane as parallel wave fronts. We know that each point along the parallel wave front must travel an equal distance to the focal point so line_b + line_c must equal a constant. If we first look at the ray that is traveling down the mirror axis we see it must travel twice the focal length to go from a wave front at the focal plane to the mirror and then return to the focus. So b + c = 2f.
If we want c we can subtract b from both sides of this equation, c = 2f - b.

We will vary r to find the surface of the parabola. Lets begin by finding b as a function of r. Using the Pythagorean Theorem, c ² = r ² + b ² . Subtracting r ² from both sides, b ² = c ² - r ². We know that c = 2f - b so lets try a substitution in order to remove ‘unknown’ c from the formula:

b ² = c ² - r ² becomes b ² = ( 2f - b ) ² - r ²

To solve for b lets multiply out c ² = ( 2f - b ) ² = ( 2f - b ) ( 2f - b ) =

( 4f ² - 4fb + b ² ).

So putting it all together we have b ² = ( 4f ² - 4fb + b ² ) - r ² .

From b ² = ( 4f ² - 4fb + b ² ) - r ² we go to:

b ² = 4f ² - 4fb + b ² - r ² then subtract b ² from both sides:

0 = 4f ² - 4fb - r ² Add r ² to both sides:

r ² = 4f ² - 4fb Factor out 4f:

r ² = 4f ( f - b ) Divide both sides by 4f:

r ² / 4f = f - b Subtract f from both sides:

( r ² / 4f ) - f = - b Multiply both sides by -1:

b = f - ( r ² / 4f )

Now that we have the formula for b suppose that we want the height, S of a point distance r from the parabola center above the height at r₀, the mirror center. S = f - b and b = f - ( r ² / 4f ) so S = f - ( f - ( r ² / 4f ) ) or:

S = r ² / 4f. Since the radius of curvature = 2f then S = r ² / 2R.

 

BACK